I. The ratio stress/strain remains constant for small deformation. What will be the effect on this ratio when the deformation made is very large?
Answer: For small deformations, the ratio stress/strain remains constant and equals the modulus of elasticity (Hooke’s Law). When deformation becomes very large, this ratio no longer remains constant. The material may exceed its elastic limit and enter the plastic region, where permanent deformation occurs. The stress-strain relationship becomes non-linear, and the material may eventually break.
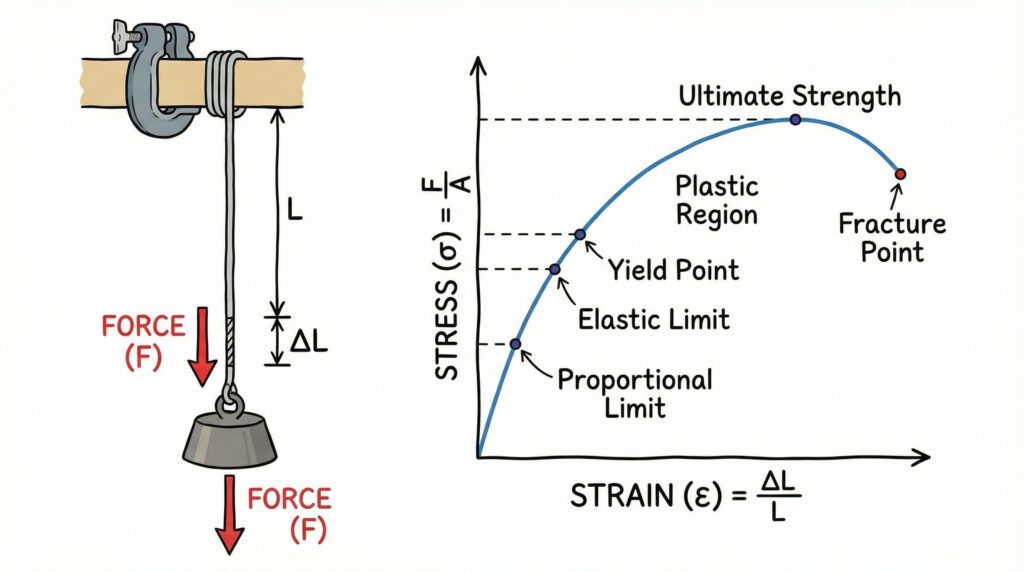
II. Define stress and strain. What are their SI units? Differentiate between tensile, compressive and shear modes of stress and strain.
Answer:
- Stress: Force per unit area applied to a body. Stress = F/A. SI unit: Pascal (Pa) or N/m²
- Strain: The ratio of the change in dimension to the original dimension. Strain = ΔL/L. SI unit: No unit (dimensionless)
Types:
- Tensile stress/strain: When force stretches the body (increases length)
- Compressive stress/strain: When force compresses the body (decreases length)
- Shear stress/strain: When a force acts tangentially, causing layers to slide over each other
III. Define modulus of elasticity. Show that the units of modulus of elasticity and stress are the same. Also discuss its three kinds.
Answer: Modulus of Elasticity: The ratio of stress to strain within the elastic limit. E = Stress/Strain = (F/A)/(ΔL/L)
Units: Since strain is dimensionless, E has the same units as stress = N/m² or Pascal (Pa)
Three types:
- Young’s Modulus (Y): For tensile/compressive stress
- Bulk Modulus (K): For volume stress (pressure)
- Shear Modulus (G): For shear stress
IV. Differentiate between elastic deformation and plastic deformation.
Answer:
- Elastic Deformation: Temporary deformation. The body returns to its original shape when the stress is removed. Occurs within the elastic limit.
- Plastic Deformation: Permanent deformation. The body does not return to its original shape when the stress is removed. Occurs beyond the elastic limit.
V. What happens if stress remains within the elastic limit, and if stress exceeds the elastic limit?
Answer:
- Within elastic limit: The body undergoes elastic deformation and returns to its original shape when stress is removed. Hooke’s law is obeyed.
- Beyondthe elastic limit: The body undergoes plastic deformation and cannot return to its original shape. Permanent deformation occurs.
VI. How is the elastic limit important in engineering?
Answer: Engineers must ensure that structures and machines operate within the elastic limit to prevent permanent deformation or failure. Knowledge of elastic limits helps in:
- Selecting appropriate materials for construction
- Determining safe load limits for structures
- Preventing structural failures and accidents
- Ensuring the longevity and reliability of engineering components
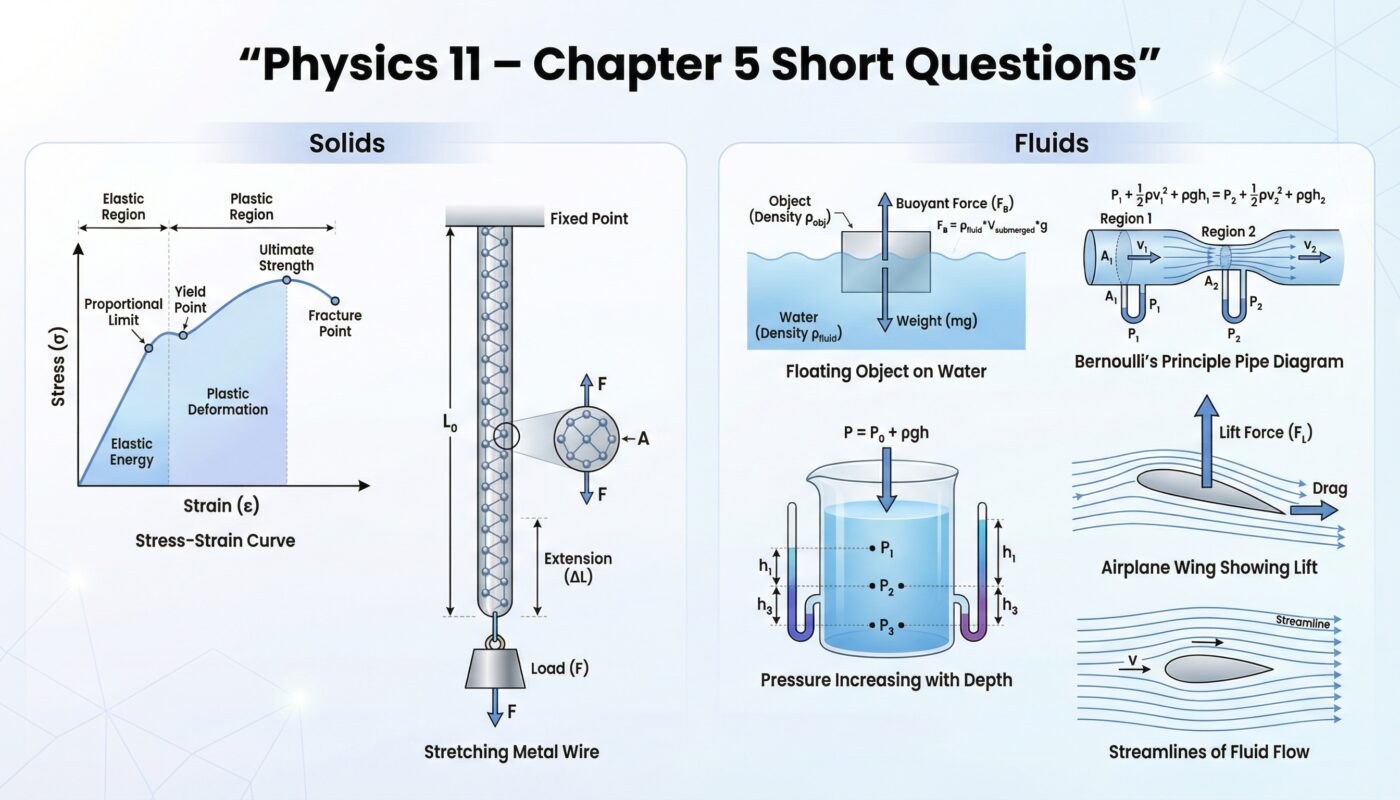
VII. Draw a stress-straincurve for a ductile material, and then define the terms: Elastic limit, Yield point and ultimate tensile stress.
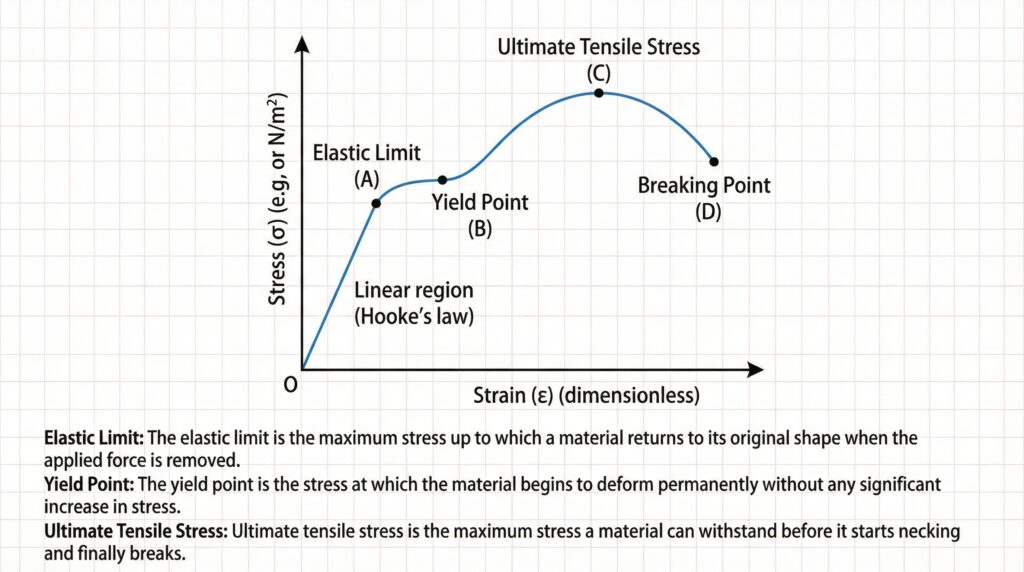
Answer: [Stress-Strain Curve Description: Shows stress on y-axis and strain on x-axis with points marked]
- Elastic Limit: The maximum stress up to which a material returns to its original shape when stress is removed
- Yield Point: The point beyond which material begins to deform plastically with little increase in stress
- Ultimate Tensile Stress: The maximum stress that a material can withstand before breaking
VIII. What is strain energy? What happens to it in plastic deformation?
Answer: Strain energy is the energy stored in a body when it is deformed elastically. In elastic deformation, this energy is fully recovered when stress is removed. In plastic deformation, strain energy is not recovered and is dissipated as heat due to internal friction between molecules.
IX. What is meant by strain energy? How can it be determined from the force-extension graph?
Answer: Strain energy is the potential energy stored in an elastic body when it is deformed. From a force-extension graph, strain energy equals the area under the curve up to the point of extension. Strain Energy = ½ × Force × Extension = Area under F-ΔL graph
X. How does pressure change with depth in fluids?
Answer: Pressure in a fluid increases linearly with depth according to the equation: P = P₀ + ρg,h, where P₀ is atmospheric pressure, ρ is fluid density, g is gravitational acceleration, and h is depth. This is because the weight of the fluid column above increases with depth.
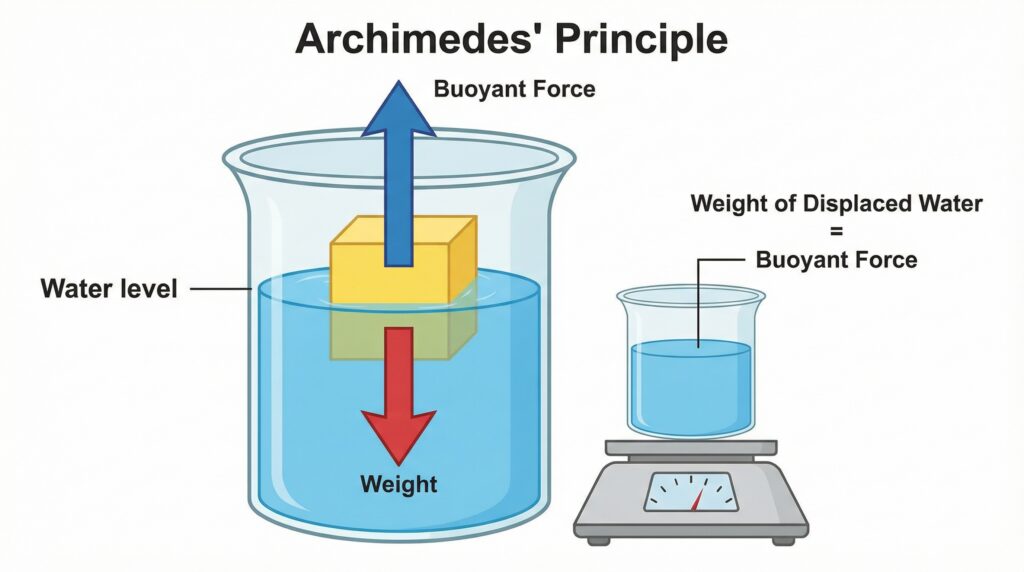
XI. How does an object float or sink according to Archimedes principle?
Answer: According to Archimedes’ principle, when an object is immersed in a fluid, it experiences an upward buoyant force equal to the weight of fluid displaced.
- Floats: If buoyant force ≥ weight of object (ρ_object < ρ_fluid)
- Sinks: If buoyant force < weight of object (ρ_object > ρ_fluid)
- Neutral buoyancy: If buoyant force = weight of object (ρ_object = ρ_fluid)
XII. How does Archimedes reportedly discover the principle that bears his name?
Answer: According to legend, King Hiero II asked Archimedes to determine if his crown was pure gold without damaging it. While bathing, Archimedes noticed that the water level rose when he entered the tub. He realised that the volume of water displaced equals the volume of the submerged object. By comparing the water displaced by the crown and an equal weight of pure gold, he could determine its purity. Excited by this discovery, he reportedly ran throughthe streets shouting “Eureka!”
XIII. Why do ships made of iron float on water?
Answer: Although iron is denser than water, ships float because of their hollow structure. The overall average density of the ship (including the air-filled interior) is less than that of water. The ship displaces a large volume of water, and the buoyant force acting upward equals the total weight of the ship, allowing it to float.
XIV. What is the condition for natural floatation?
Answer: For natural floatation, the weight of the object must equal the weight of fluid displaced by its submerged portion. Mathematically: Weight of object = Buoyant force Or: ρ_object × V_object × g = ρ_fluid × V_submerged × g The average density of the floating object must be less than or equal to the fluid density.
XV. Differentiate between streamline and turbulent flow of a fluid.
Answer: Streamline Flow (Laminar Flow):
- Fluid particles move in parallel layers
- Velocity at each point remains constant
- No mixing between layers
- Occurs at low velocities
- Energy is conserved
Turbulent Flow:
- Fluid particles move in irregular, chaotic paths
- Velocity at each point fluctuates
- Mixing occurs between layers
- Occurs at high velocities
- Energy is lost due to friction
XVI. How is variation in pressure related to the speed of a fluid?
Answer: According to Bernoulli’s principle, pressure and velocity of a fluid are inversely related. When fluid velocity increases, its pressure decreases, and vice versa. This is expressed in Bernoulli’s equation: P + ½ρv² + ρgh = constant. Where high-velocity regions have low pressure, and low-velocity regions have high pressure.
XVII. What is meant by ideal fluid? State conditions to be satisfied byan ideal fluid.
Answer: An ideal fluid is a hypothetical fluid used to simplify fluid dynamics problems.
Conditions for ideal fluid:
- Incompressible: Density remains constant
- Non-viscous: No internal friction between fluid layers
- Irrotational: No rotational motion of fluid particles
- Steady flow: Velocity at any point does not change with time
XVIII. How can laminar flow be changed into turbulent flow?
Answer: Laminar flow can be changed to turbulent flow by:
- Increasing the velocity of fluid beyond the critical velocity
- Increasing the diameter of the pipe
- Decreasing the viscosity of the fluid
- Creating obstacles or rough surfaces in the flow path. This occurs when the Reynolds number exceeds approximately 2000.
XIX. Does velocity remain constant along a streamline in steady flow?
Answer: No, velocity does not necessarily remain constant along a streamline in steady flow. However, the velocity at a fixed point on the streamline remains constant with time. Along the streamline, velocity can change according to Bernoulli’s equation. If the cross-sectional area changes, velocity changes to maintain continuity (equation of continuity: A₁v₁ = A₂v₂).
XX. What is the equation of continuity? What does it imply?
Answer: The equation of continuity states that for an incompressible fluid in steady flow: A₁v₁ = A₂v₂ = constant or ρAv = constant
Implications:
- Mass flow rate remains constant throughout the pipe
- Wherethe cross-sectional area is small, the velocity is high
- Where the cross-sectional area is large, the velocity is low
- This represents conservation of mass
XXI. Give a real-life example where the equation of continuity is observed.
Answer: When water flows through a garden hose, and we partially close the nozzle opening with our thumb, the water shoots out faster and farther. This is because reducing the cross-sectional area increases the velocity of water to maintaina constant flow rate (A₁v₁ = A₂v₂). Other examples include blood flow in arteries and veins, and river flow through narrow channels.
XXII. State Bernoulli’s equation for a liquid in motion and describe some of its applications.
Answer: Bernoulli’s Equation: P + ½ρv² + ρgh = constant Or: P₁ + ½ρv₁² + ρgh₁ = P₂ + ½ρv₂² + ρgh₂
Applications:
- Working of atomisers and sprayers
- Airfoil design (aeroplane wings)
- Venturi meter for measuring fluid flow
- Carburettor in automobiles
- Magnus effect in sports
- Sailing boats and spinning balls
XXIII. A person is standing near a fast-moving train. Is there any danger that he will fall towards it?
Answer: Yes, there is danger. According to Bernoulli’s principle, fast-moving air between the person athe nd train has lower pressure than the stationary air on the other side of the person. This pressure difference creates a net force pushing the person toward the train. The person may lose balance and fall toward the moving train, which is extremely dangerous.
XXIV. Two row boats moving parallel in the same direction are pulled towards each other. Explain.
Answer: When two boats move parallel and close to each other, the water between them moves faster than the water on their outer sides. According to Bernoulli’s principle, faster-moving water has lower pressure. The pressure difference creates a net inward force on both boats, pulling them toward each other. This is similar to the attraction between parallel-moving objects in fluids.
XXV. What is Bernoulli’s equation? What does it represent?
Answer: Bernoulli’s equation is: P + ½ρv² + ρgh = constant
It represents:
- Conservation of energy for flowing fluids
- P (pressure energy per unit volume)
- ½ρv² (kinetic energy per unit volume)
- ρgh (potential energy per unit volume)
- The sum of these three energies remains constant along a streamline for an ideal fluid.d
XXVI. According to Bernoulli’s theorem, the pressure of a fluid should remain uniform in a pipe of a uniform radius. But actually, it goes on decreasing. Why is it so?
Answer: In an ideal fluid with no viscosity, pressure would remain constant in a horizontal uniform pipe. However, real fluids have viscosity (internal friction). As fluid flows through the pipe, energy is lost due to:
- Viscous friction between fluid layers
- Friction between the fluid and the pipe wall. This energy loss appears as heat, reducing pressure along the length of the pipe. Bernoulli’s equation applies only to ideal fluids.
XXVII. Whyis standing near a fast-moving train dangerous? Explain briefly.
Answer: Standing near a fast-moving train is dangerous due to Bernoulli’s principle. When a train moves at high speed:
- Air between the train and the person moves very fast (dragged by the train)
- According to Bernoulli’s principle: P + ½ρv² = constant
- Fast-moving air has LOW PRESSURE
- Air on the opposite side of a person is stationary with NORMAL atmospheric pressure.
- Pressure difference: P_stationary > P_fast-moving
- Net force pushes person TOWARD the train
- A person can lose balance and be pulled into the train’s path
This is why safety lines are marked on railway platforms.
XXVIII. Explain how the swing is produced in a fast-moving cricket ball?
Answer: Swing bowling uses Bernoulli’s principle and the asymmetric ball condition:
Conventional Swing:
- Bowler keeps ONE side shiny/smooth and the OTHER side rough/worn
- Smooth side: Air flows smoothly → HIGHER velocity → LOWER pressure
- Rough side: Air turbulent/disturbed → LOWER velocity → HIGHER pressure
- Pressure difference creates a sideways force
- The ball swings from the high-pressure side to the low-pressure side
- Seam position helps create asymmetric airflow
XXIX. Explain the working of a carburettor of a motor car using Bernoulli’s principle.
Answer: A carburettor mixes air and petrol using Bernoulli’s principle:
Working mechanism:
- Air inlet: Air enters through the carburettor passage
- Venturi throat: Passage narrows (constriction/venturi)
- Velocity increases: By equation of continuity (A₁v₁ = A₂v₂), when area decreases, velocity increases
- Pressure drops: By Bernoulli’s equation (P + ½ρv² = constant), when velocity increases, pressure decreases
- Fuel suction: Low pressure at the throat sucks petrol from the fuel chamber through a jet/nozzle
- Atomization: High-velocity air breaks fuel into fine droplets (mist)
- Mixture formation: Air-fuel mixture (about 15:1 ratio) enters the engine cylinder
Key principle: HIGH velocity → LOW pressure → SUCTION of fuel
This ensures proper fuel-air mixing for efficient combustion in the engine.
XXX. When water fallsfrom thea top, itscross-sectionall area decreases as it comes down. Explain.
Answer: The narrowing of the water stream is explained by the equation of continuity:
Step-by-step explanation:
- Initial condition: Water starts falling with initial velocity v₁ and cross-sectional area A₁
- Acceleration: As water falls through height h, gravity accelerates it
- Using: v₂² = v₁² + 2gh
- Velocity INCREASES as it falls
- Equation of continuity: For incompressible fluid (water):
- A₁v₁ = A₂v₂ = constant (volume flow rate constant)
- Mass flow rate: ρA₁v₁ = ρA₂v₂
- Result: When v₂ > v₁ (velocity increases)
- Then A₂ must be < A₁ (area must decrease)
- To keep Av = constant
- Conclusion: Cross-sectional area decreases as water falls and gains speed
XXXI. What is the significance of Bernoulli’s equation due to the pressure difference?
Bernoulli’s equation shows that an increase in fluid speed is associated with a decrease in pressure. This pressure difference explains fluid flow, lift on aeroplane wings, and suction effects in devices such as atomisers and carburettors
Answer: The significance of the pressure difference in Bernoulli’s equation is:
- It explains how energy converts between pressure, kinetic, and potential forms in flowing fluids
- High-velocity regions have low pressure and vice versa
- This pressure difference creates forces that explain many phenomena, such as lift on aeroplanes’ wings, the attraction between moving objects, the operation of venturi meters, and the operation of atomisers.
- It is fundamental to understanding fluid dynamics in engineering applications.s
XXXII. Why are the wings of an aeroplane round outward while flattened inward?
Answer: Aeroplanee wings (airfoils) are designed with a curved upper surface and flatter lower surface to create lift:
- Air travelling over the curved upper surface has to cover a longer path
- This air moves faster than air below the wing (continuity principle)
- By Bernoulli’s principle, faster-moving air above has lower pressure
- Slower-moving air below has higher pressure
- The pressure difference creates an upward lift force that supports the aeroplane in flight
XXXIII. Name one application forStokes’s law to apply.
Answer: One important application of Stokes’ law is determining the terminal velocity of small spherical objects falling through viscous fluids, such as:
- Measuring the viscosity of liquids in laboratories
- Understanding the sedimentation of particles in liquids
- Studying the motion of raindrops through the air
- Centrifugation processes in laboratories
XXXIV. What is terminal velocity?
Answer: Terminal velocity is the constant maximum velocity attained by an object falling through a viscous medium (like air or a liquid) when the upward viscous drag force and buoyant force balance the downward gravitational force. At terminal velocity, the net force is zero, and the acceleration stops, so the object continues falling at constant speed.
XXXV. Why does an object reach terminal velocity?
Answer: An object reaches terminal velocity because:
- Initially, gravitational force pulls the object downward, causing acceleration
- As velocity increases, the viscous drag force (opposing motion) also increases
- Eventually, drag force plus buoyant force equals gravitational force
- Net force becomes zero, stopping further acceleration
- Object continues at constant velocity (terminal velocity). This occurs according to: Weight = Drag force + Buoyant force